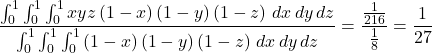Here the problem is to find the average volume of a rectangular solid inside a unit cube if all the faces are parallel to the coordinate planes.
The average length of each edge
should be about ![]() , so the average volume should be about
, so the average volume should be about ![]() .
.
Results of an experiment with ![]() trials repeated
trials repeated ![]() times:
times:
| 0.0371114 | 0.0370923 | 0.0370093 | 0.0369729 | 0.0371264 |
| 0.0370046 | 0.0370573 | 0.0370841 | 0.0369732 | 0.0371046 |
Consider a rectangular solid of dimensions ![]() . The probability of picking such a rectangular solid should be proportional to the volume
. The probability of picking such a rectangular solid should be proportional to the volume ![]() of the small rectangular solid. The average volume is
of the small rectangular solid. The average volume is