Unit Cube

We look at the average distance between two points inside the unit cube. Here are 20 line segments whose endpoints are randomly chosen inside the unit cube:

 

The average distance between the two points \left( x,y,z\right) and \left( r,s,t\right) should be roughly the diagonal of an average cube, which should have edge about 1/3, so the diagonal should be about

    \begin{equation*}\sqrt{3}/3= 0.577\,350\,269\,2\end{equation*}

Here are the results of a simulation with 10 trials of 1000\,000:

    \[0.66145671 \qquad 0.66165457 \qquad 0.66161102 \qquad 0.66194795 \qquad 0.66168745\]


    \[0.66190286 \qquad 0.66188905 \qquad 0.66192821 \qquad 0.66173251 \qquad 0.6623762\]

Consider points \left( x,y,z\right) and \left( r,s,t\right) in the unit cube. The average distance between the two points is given by

    \begin{eqnarray*}&&\frac{\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\sqrt{\left( x-r\right) ^{2}+\left( y-s\right) ^{2}+\left(z-t\right) ^{2}}\,dx\,dy\,dz\,dr\,ds\,dt}{\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\,dx\,dy\,dz\,dr\,ds\,dt} \\&=&\frac{1}{105}\left( 4+17\sqrt{2}-6\sqrt{3}+21\ln \left( 1+\sqrt{2}\right)+42\ln \left( 2+\sqrt{3}\right) -7\pi \right) \\&\approx &0.661\,707\,182\,3\end{eqnarray*}

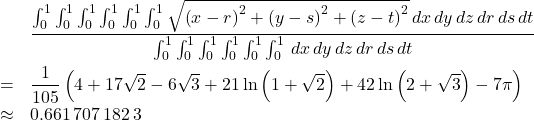
Alternatively, assume that x, y, and z are the dimensions of a box
whose opposite vertices are two points in the unit cube. Note that this
small cube can be moved inside the unit cube as long as the point closest to
the point \left( 1,1,1\right) remains inside a box of dimensions \left(1-x\right) \times \left( 1-y\right) \times \left( 1-z\right). The average
length of the diagonal of such a box is

    \begin{equation*}\frac{\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\sqrt{x^{2}+y^{2}+z^{2}}\left(1-x\right) \left( 1-y\right) \left( 1-z\right) \,dz\,dy\,dx}{\int_{0}^{1}\int_{0}^{1}\int_{0}^{1}\left( 1-x\right) \left( 1-y\right)\left( 1-z\right) \,dz\,dy\,dx}\approx 0.661\,707\,182\, 3\end{equation*}


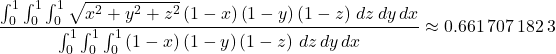
This may not be much easier to evaluate, but at least we’ve reduced the
number of integral signs and the number of variables.

This number, called the Robbins constant, was computed by D. P. Robbins in
the American Mathematical Monthly in 1978. See Weisstein, Eric W. “Cube Line
Picking.” From MathWorld–A Wolfram Web Resource.
http://mathworld./wolfram.com/CubeLinePicking.html