What is the average distance between two points inside the unit square? The picture shows 20 pairs of random points, shown as the endpoints of straight line segments.
Here are the results of an experiment with ![]() trials repeated
trials repeated ![]() times:
times:
![]()
Let ![]() be difference in there first coordinates and
be difference in there first coordinates and ![]() the difference in their second coordinates. The larger first coordinate can be chosen anywhere in an interval of length
the difference in their second coordinates. The larger first coordinate can be chosen anywhere in an interval of length ![]() , and the larger second coordinate can be chosen anywhere in an interval of length
, and the larger second coordinate can be chosen anywhere in an interval of length ![]() .
.
The probability of picking a rectangle of this size and shape should be proportional to the area ![]() of the red rectangle.
of the red rectangle.
The distance between the two endpoints is ![]() . The average distance is
. The average distance is

We could make this a bit more ugly by taking two points ![]() and
and ![]() in the unit square and evaluating
in the unit square and evaluating
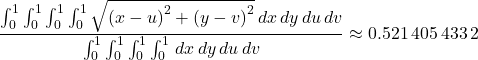
See http://mathworld.wolfram.com/SquareLinePicking.html for more details.

