Unit Interval

Here is an example of an average calculus problem suggested by David Yu of Fort Collins, Colorado. Suppose that two numbers are chosen at random between 0 and 1. How far apart do we expect these two numbers to be?
The first step is to try to understand the problem, perhaps by drawing some pictures. Here is a picture of 10 pairs of randomly chosen numbers between 0 and 1. The random numbers are endpoints of the line segments.

AverageDistance1

Think about the problem and try to solve it. At least determine what a reasonable answer might be. Here is a very naïve approach: If the first number is 0 or 1, then the
average for the second number should be about 1/2, so the distance between
the two numbers should be about 1/2. On the other hand, if the first
number is 1/2, then the second number is either between 0 and 1/2, or
between 1/2 and 1. In either case, the average distance between the two
numbers should be about 1/4. So the answer to the initial problem must be
between 1/4 and 1/2. The Farey mean

    \begin{equation*} \frac{1+1}{4+2}=\frac{2}{6}=\frac{1}{3} \end{equation*}

provides a reasonable guess for the average distance between two numbers chosen at random.

The next step might be to do some experiments using random numbers. Pick two
numbers between 0 and 1 and compute the distance between them. Repeat
this 1\,000\,000 times and add together all of the distances. Divide by 1\,000\,000 and get 0.333\,168\,38 as an estimate for the average distance
between two numbers. Repeat this process 10 times. Here are the results:

    \[0.33316838 \qquad 0.33333392 \qquad 0.33339517 \qquad 0.33329333 \qquad 0.33325102\]

    \[0.33346554 \qquad 0.33364919 \qquad 0.33315781 \qquad 0.33320678 \qquad 0.33364789\]

If these numbers acted like complete strangers, that would cause doubts.
However, these numbers are quite compatible. They all look like close friends
of our original guess 1/3.

Now use some calculus and see if 1/3 stands up as a likely solution. Let % x be the length of an interval that represents the distance between two
points. Then the larger endpoint can be chosen anywhere in a interval of
length 1-x. The probability of picking a line segment of length x should
be proportional to 1-x. The integral \int_{0}^{1}x\left( 1-x\right) \,dx
represents the sum of the possible lengths x together with the frequency
with which each such length occurs. The frequency with which all possible
lengths occur is given by the integral \int_{0}^{1}\left( 1-x\right) \,dx.
In the discrete case, an average of numbers x_{1}, x_{2}, \ldots, % x_{n} is given by the quotient

    \begin{equation*} \frac{x_{1}+x_{2}+\cdots x_{n}}{n} \end{equation*}

The calculus equivalent uses the quotient

    \begin{equation*} \frac{\int_{0}^{1}x\left( 1-x\right) \,dx}{\int_{0}^{1}\left( 1-x\right) \,dx }=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3} \end{equation*}

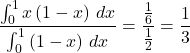
where the numerator represents of sum of all possible lengths together with
their frequencies and the denominator represents the sum of the frequencies.

Alternatively, assume that x and y are the endpoints of an interval
inside the unit interval. Then \left\vert x-y\right\vert is the distance
between the two endpoints. The average distance between the points x and % y in the unit interval is given by

    \begin{equation*} \frac{\int_{0}^{1}\int_{0}^{1}\left\vert x-y\right\vert \,dy\,dx}{% \int_{0}^{1}\int_{0}^{1}\,dy\,dx}=\int_{0}^{1}\int_{0}^{1}\left\vert x-y\right\vert \,dy\,dx \end{equation*}

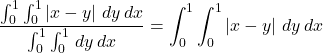
since the integral in the denominator is equal to 1. The absolute value
can be eliminated by decomposing the unit square into two disjoint
triangular regions and rewriting the integral as a sum

    \begin{eqnarray*} \int_{0}^{1}\int_{0}^{1}\left\vert x-y\right\vert \,dy\,dx &=&\int_{0}^{1}\int_{0}^{x}\left( x-y\right) \,dy\,dx+\int_{0}^{1}\int_{x}^{1}\left( y-x\right) \,dy\,dx \\ &=&\frac{1}{6}+\frac{1}{6}=\frac{1}{3} \end{eqnarray*}

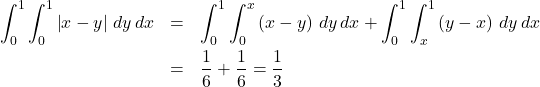
By this time, confidence in the answer 1/3 should be running high.