To find the average area of a square in the unit square, assume again that the edges are parallel to the coordinate axes. Here is a picture of 10 randomly chosen squares:
As with the rectangle, it would appear that an average edge of a square should be about 
, so the average area should be about 
. This worked for rectangles, so it should work here as well.
The following results of an experiment with 
trials repeated 
times are just a bit of a surprise. Why should the average area of a square be less than the average area of a rectangle?
When you guess wrong, it is always tempting to go back and rationalize why
the unexpected result might be reasonable. In this case, although the
average area of a rectangle is exactly the area of a square with average
dimensions, in reality most rectangles appear to be long and skinny, whereas
squares are always square. The rigidity of squares means there aren’t as
many, and the average area is less. At least it’s possible to see that the
answers might be different.
Consider a square of edge 
. By placing this square in the lower left
corner of the unit square, we see that the upper right corner could be moved
to anywhere inside a square of edge 
. The probability of picking a
square of edge should be proportional to the area 
of the blue square.
The average area is given by
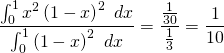
In contrast to the previous problem, the average area of a square does not
reduce to the one-dimensional case.