 What is the average area of a rectangle inside the unit square if the edges of the rectangle are parallel to the coordinate axes. Here is a picture of 10 trials:
What is the average area of a rectangle inside the unit square if the edges of the rectangle are parallel to the coordinate axes. Here is a picture of 10 trials:
Think of ![]() and
and ![]() as lengths of average intervals in the unit interval and think of two opposite vertices of a rectangle with sides
as lengths of average intervals in the unit interval and think of two opposite vertices of a rectangle with sides ![]() and
and ![]() .
.
The average value of ![]() should
should
be ![]() , and the average value of
, and the average value of ![]() should be
should be ![]() , so the average area
, so the average area
of a rectangle should be about ![]() .
.
Do an experiment by picking two points ![]() and
and ![]() in the unit square and take those two points to be opposite
in the unit square and take those two points to be opposite
vertices of a rectangle. The area of such a rectangle is ![]() . Repeat this experiment
. Repeat this experiment ![]() times, add together all of the areas and divide by
times, add together all of the areas and divide by ![]() . A
. A
typical average is ![]() . Repeat this
. Repeat this ![]() times and record the
times and record the
results. The numbers
![]()
are all very close to our guess of ![]() .
.
To find a calculus solution to this problem, consider a rectangle with edges
![]() and
and ![]() . Such a rectangle can be moved rigidly anywhere so long as the
. Such a rectangle can be moved rigidly anywhere so long as the
upper right corner lies within a rectangle with edges ![]() and
and ![]() . The
. The
probability of picking a rectangle with edges ![]() and
and ![]() should be
should be
proportional to the area ![]() of the blue
of the blue
rectangle.
The average area of a rectangle in the unit square is
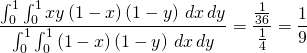
where the numerator represents the areas ![]() together with their
together with their
frequencies and the denominator represents the total frequencies. This
answer is not a surprise since
![]()
and hence the problem reduces completely to two instances of the
one-dimensional problem.
Alternatively, the average area is given by the integral
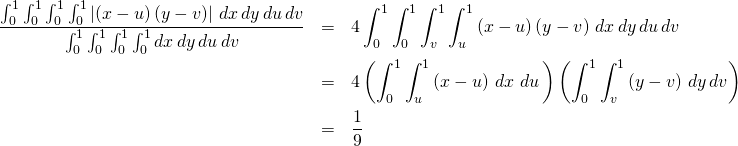
where ![]() is the
is the
area of a rectangle with opposite corners ![]() and
and ![]() . The answer
. The answer ![]() is looking good.
is looking good.


