What is the average volume of a tetrahedron whose four vertices are chosen at random inside the unit cube? Here is a picture of one such tetrahedron.
Here is the result of ![]() trials repeated
trials repeated ![]() times:
times:
![]()
The volume of the tetrahedron with vertices ![]() ,
, ![]() ,
, ![]() ,
, ![]() is given by
is given by
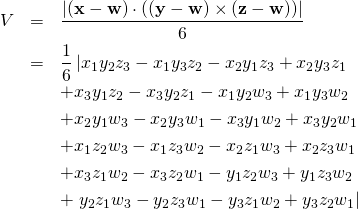
The average volume of the tetrahedron in the unit cube is given by the
iterated integral
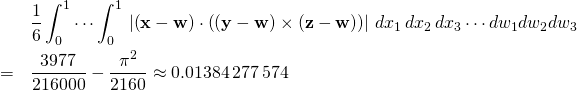
That’s right, there are ![]() integral signs and
integral signs and ![]() variables.
variables.

