Unit Circle

Here we look at the average distance between two points inside the unit circle. The following is a picture of 10 line segments whose endpoints are randomly chosen inside the unit circle.

Here are the results of 1\,000\,000 trials, repeated 10 times:

    \begin{equation*} \begin{array}{ccccc} 0.90439210 & 0.90567635 & 0.90637156 & 0.90585888 & 0.90613175 \\ 0.90534573 & 0.90549458 & 0.90658781 & 0.90519532 & 0.90511214 \end{array} \end{equation*}

Pick r and \theta at random in the intervals 0\leq r\leq 1 and 0\leq\theta \leq 2\pi. The points \left( r\cos \theta ,r\sin \theta \right) tend to be bunched at the center, whereas the points \left( \sqrt{r}\cos\theta ,\sqrt{r}\sin \theta \right) are uniformly distributed within the unit disk.

Note that the area inside the circle \left( \sqrt{1/2}\cos \theta ,\sqrt{1/2}\sin \theta \right) is exactly half the area of the unit circle since

    \begin{equation*} \pi r^{2}=\pi \left( \sqrt{1/2}\right) ^{2}=\frac{1}{2}\pi \end{equation*}

In a similar manner, the area inside the circle \left( \sqrt{r}\cos \theta , \sqrt{r}\sin \theta \right) has area

    \begin{equation*} \pi \left( \sqrt{r}\right) ^{2}=\pi r \end{equation*}

and hence the ratio of its area to the unit circle is exactly r:1.

Without loss of generality, pick one point \left( \sqrt{s},0\right) on the positive x-axis and a second point \left( \sqrt{r}\cos \theta ,\sqrt{r}\sin \theta \right) uniformly within the unit disk. The distance between these two points is

    \begin{eqnarray*} \sqrt{\left( \sqrt{s}-\sqrt{r}\cos \theta \right) ^{2}+\left( \sqrt{r}\sin \theta \right) ^{2}} &=&\sqrt{s+r\cos ^{2}\theta +r\sin ^{2}\theta -2\sqrt{r} \sqrt{s}\cos \theta } \\ &=&\sqrt{s+r-2\sqrt{r}\sqrt{s}\cos \theta } \end{eqnarray*}

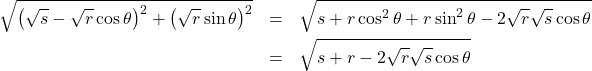
The average distance between two points is given by

    \[\frac{\int_{0}^{1}\int_{0}^{1}\int_{0}^{2\pi }\sqrt{s+r-2\sqrt{r}\sqrt{s} \cos \theta }\,dr\,ds\,d\theta }{\int_{0}^{1}\int_{0}^{1}\int_{0}^{2\pi } \,dr \,ds \,d\theta } = \frac{128}{45\pi }\approx 0.905\,414\,787\, 4\]