Rotated Square

This problem allows the squares to be rotated inside the unit square.

RotatedSquare

On the surface, it would seem that the average area of a rotated square should be somewhat smaller than the average for squares whose edges are parallel to the coordinate axes. However, here are the results of an experiment with 1000\,000 trials repeated 10 times:

    \begin{equation*} \begin{array}{ccccc} 0.13329815 & 0.13276880 & 0.13298214 & 0.13360482 & 0.13305544 \\ 0.13375200 & 0.13327872 & 0.13321189 & 0.13290105 & 0.13387584% \end{array}% \end{equation*}

Again, the surprise sparks a reassessment of the original guess. Although
the largest square must have edges (nearly) parallel to the coordinate axes,
moderate sized squares can be rotated through any angle and remain within
the unit square. Thus moderate sized squares tend to appear with greater
frequencies, hence the average area might very well be larger.

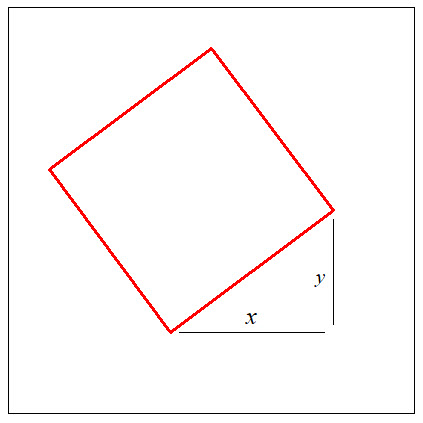
Consider a typical rotated square, and assume x and y are given as in
the picture.

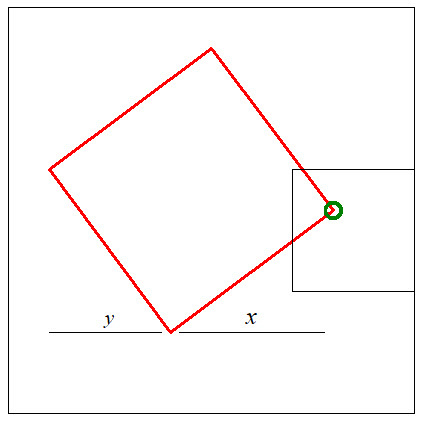
The red square can be moved rigidly so that the green vertex  is
anywhere inside a square of edge 1-x-y.

The probability of
picking a square of this size and orientation is proportional to the area % \left( 1-x-y\right) ^{2} of the red square. The length of an edge is \sqrt{% x^{2}+y^{2}} and hence the area of the green square is x^{2}+y^{2}. The
average area is given by

    \begin{equation*} \frac{\int_{0}^{1}\int_{0}^{1-x}\left( x^{2}+y^{2}\right) \left( 1-x-y\right) ^{2}dy\,dx}{\int_{0}^{1}\int_{0}^{1-x}\left( 1-x-y\right) ^{2}dy\,dx}=\frac{\frac{1}{90}}{\frac{1}{12}}=\frac{2}{15}\approx 0.1\bar{3} \end{equation*}

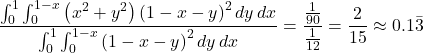
This is certainly consistent with the experimental results.