Rectangular Equations

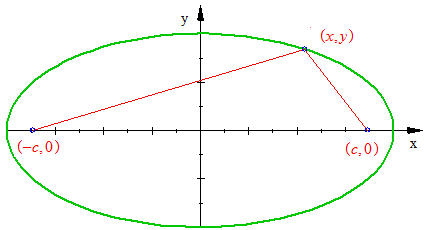
Suppose that the foci of an ellipse are located at the points (-c,0) and (c,0). Denote the sum of the distances from a point on the ellipse to the foci by 2a. Set b=\sqrt{a^2-c^2}.Ellipse

A point (x,y) lies on the ellipse if

    \[\sqrt{(x-c)^2+(y-0)^2} + \sqrt{(x-(-c))^2 +(y-0)^2}=2a\]

which can be rewritten in the form

    \[\sqrt{(x-c)^2+(y-0)^2} = 2a-\sqrt{(x-(-c))^2 +(y-0)^2}\]

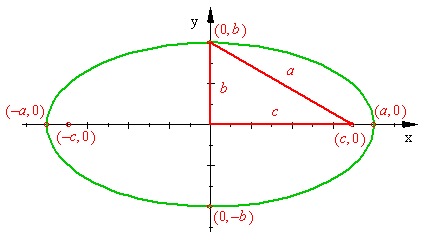
Ellipse2
Square both sides of the equation to get

    \[x^2 -2cx+c^2+y^2=4a^2-4a\sqrt{x2+2xc+c^2} +x^2+2xc+c^2+y^2\]

which simplifies to

    \[cx+a^2=a\sqrt{c^2+2cx+x^2+y^2}\]

Square both sides again to get

    \[c^2x^2+2a^2cx+a^4=a^2(c^2+2cx+x^2+y^2)\]

Use the fact that c^2=a^2-b^2 to obtain the equation

    \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\]

Similar steps can be used to find the equation of an ellipse if the foci are located at the points (0,c) and (0,-c) on the y-axis. This time, let 2b denote the sum of the distance and set a=\sqrt{b^2-c^2}.
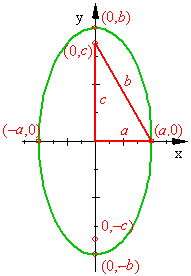Ellipse3The equation

    \[\sqrt{(x-0)^2+(y-c)^2}+\sqrt{(x-0)^2+(y-(-c))^2}=2b\]

can be rewritten in the form

    \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\]

The standard equation for an ellipse with center (h,k) and semi-axes a and b is given by

    \[\frac{\left( x-h\right) ^{2}}{a^{2}}+\frac{\left( y-k\right) ^{2}}{b^{2}}=1\]