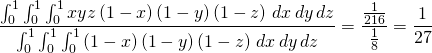Here the problem is to find the average volume of a rectangular solid inside a unit cube if all the faces are parallel to the coordinate planes. Here are four trials:
The average length of each edge
should be about ![]() , so the average volume should be about
, so the average volume should be about ![]() .
.
Results of an experiment with ![]() trials repeated
trials repeated ![]() times:
times:
![]()
Observe that
![]()
Let ![]() and
and ![]() be opposite vertices
be opposite vertices
of a rectangular solid. The volume is
![]()
and hence the expected volume is given by
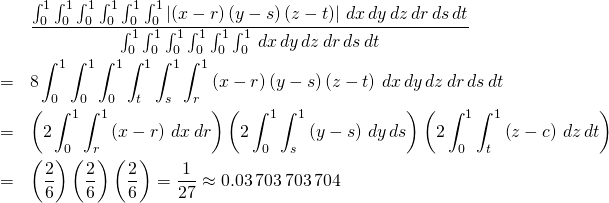
Notice that the solution reduced to three instances of the one-dimensional
case based on the average distance between two points.
Alternatively, consider a rectangular solid of dimensions ![]() . The probability of picking such a rectangular solid should be proportional to the volume
. The probability of picking such a rectangular solid should be proportional to the volume ![]() of the blue rectangular solid. The average volume is
of the blue rectangular solid. The average volume is