 What is the average area of a triangle whose vertices are randomly chosen inside the unit square? Here is a picture of 10 random triangles.
What is the average area of a triangle whose vertices are randomly chosen inside the unit square? Here is a picture of 10 random triangles.
Results of an experiment with ![]() trials repeated
trials repeated ![]() times:
times:
![]()
The triangle with vertices ![]() ,
, ![]() , and
, and ![]() has area
has area
![]()
The expected area is given by
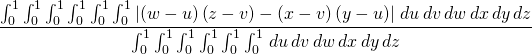
The absolute values can be removed by decomposing this cube into disjoint
regions, obtaining an average area of
![]()
